Never. Edit (4/20/2017): Well, maybe in limited circumstances.
Month: March 2017
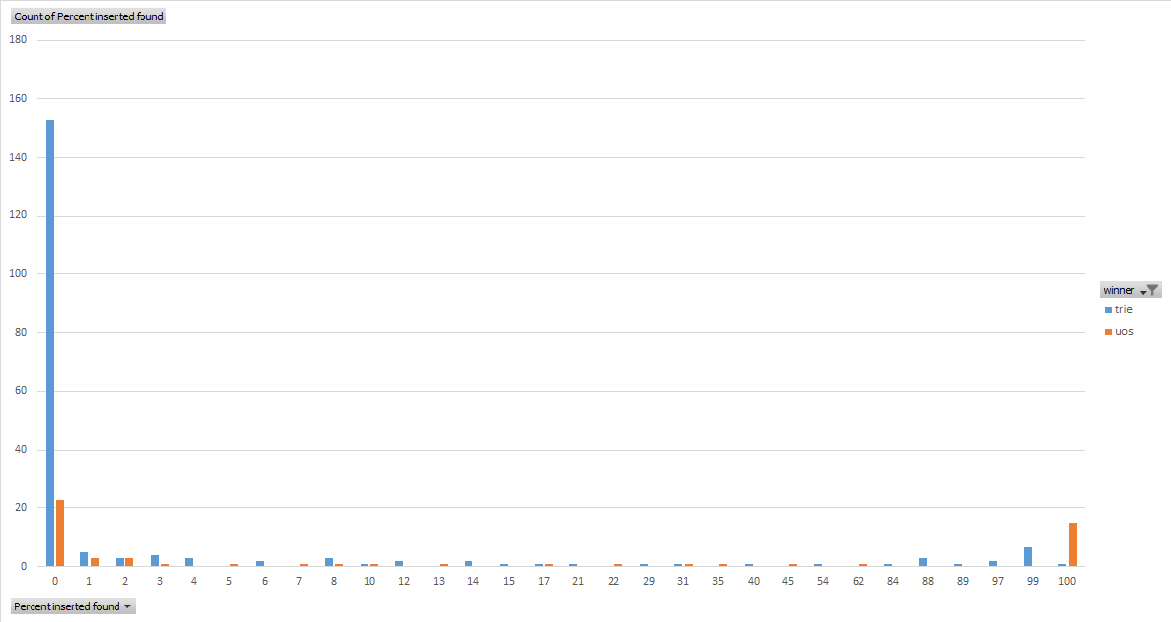
Performance comparison: std::set vs. std::unordered_set vs. custom trie
I recently interviewed with a large company where I was asked how I would check that a given word was a valid English word. Knowing that there were on the order of a few tens of thousands of stems, and that each stem may have many variations, I figured that there were maybe a few hundred thousand possible words in the English language. With each word having average length probably in the 7 range, there might be a million or so characters in this set. I concluded that the check could be performed by searching an in-memory dictionary, and proposed either a std::unordered_set, or a custom trie, with a performance test necessary to see which would be faster.
I decided to perform this test.
Algorithm: Can a string be covered by the elements in a set?
I recently was asked essentially this question in an interview: given a string S and a set of strings P, can the strings from P be concatenated with repetitions to form S? Or put another way, can strings from P with repetitions cover S without overlaps?
My first instinct was to use suffix tries and an overlap graph, but the solution that we eventually reached used no sophisticated data structures, just the array of strings and some recursion in a divide and conquer approach. Here’s my extended thoughts on the problem.
When to use it: Tries
I’ll admit it up front, this is not as much of a “when to use it” post as it is a “what is it” post. Never fear, I’ll still fill you all in on when to use it. Also, I’m talking about the data structure for storing strings, not the synonym for attempts.
What is it?
A trie is a data structure that is used for fast string searching. A trie has a root node, and a node for each character in the string. The nodes are constructed such that traversing the tree from the root to a leaf reconstructs one of the strings that is stored in it.