I recently interviewed with a large company where I was asked how I would check that a given word was a valid English word.  Knowing that there were on the order of a few tens of thousands of stems, and that each stem may have many variations, I figured that there were maybe a few hundred thousand possible words in the English language.  With each word having average length probably in the 7 range, there might be a million or so characters in this set.  I concluded that the check could be performed by searching an in-memory dictionary, and proposed either a std::unordered_set, or a custom trie, with a performance test necessary to see which would be faster.

I decided to perform this test.

Methodology

I decided to actually perform two tests: element addition performance, and element checking performance.

I wrote a simple Windows C++ application using the Windows performance analysis technique I described in a gist.  In this simple C++ application, lines from an input file are added into the data structure, and lines from another input file are used to search the data structure.  The application outputs a single CSV line containing information such as the number of elements added to the DS, the number of elements for which a search was performed, the number of elements found in the data structure, time to add all elements to the data structure, time to search for all elements, and more.

Then I wrote a python script to call the C++ application using slightly modified input files from the Moby Words II data set.  The data set was modified so that the files contained only letters in the ASCII table between space and tilde.  This seemingly corrected errors in the text, and allowed each trie node to have a smaller range of allowable children.  Each of the 16 files in the data set is paired with each of the 16 files in the data set as both an input and output, for a total of 256 tests.

The files in the data set can be summarized as follows, courtesy of Project Gutenberg’s description :

• acronyms.txt: 6,213 acronyms
  common acronyms & abbreviations
• common.txt: 74,550 common dictionary words
  A list of words in common with two or more published dictionaries.
  This gives the developer of a custom spelling checker a good
  beginning pool of relatively common words.
• compound.txt: 256,772 compound words
  Over 256,700 hyphenated or other entries containing more than one
  word as well as all capitalized words and acronyms. Phrases were
  considered ‘common’ if they or variations of them occur in standard
  dictionaries or thesauruses.
• crosswd.txt: 113,809 official crosswords
  A list of words permitted in crossword games such as Scrabble(tm).
  Compatible with the first edition of the Official Scrabble Players
  Dictionary(tm). Since this list has all forms: -ing, -ed, -s, and so
  on of words, it makes a good addition when building a custom spelling
  dictionary.
• crswd-d.txt: 4,160 official crosswords delta
  When combined with the 113,809 crosswords file, it produces the
  official crossword list compatible with the second edition of the
  Official Scrabble Players Dictionary. (Scrabble is a registered
  trademark of Milton-Bradley licensed to Merriam-Webster.)
• fiction.txt: 467 current fiction substrings
  The most frequently occurring 467 substrings occurring in a
  best-selling novel by Amy Tan in 1990.
• freq.txt: 1,000 by frequency
  This file consists of the 1,000 most frequently used English words
  from a wide variety of common texts listed in decreasing order of
  frequency
• freq-int.txt: 1,000 by frequency internet
  This file consists of the 1,000 most frequently used English words
  as used on the Internet computer network in 1992.
• KJVfreq.txt: 1,185 King James Version frequent substrings
  The most frequently occurring 1,185 substrings in the King James
  Version Bible ranked and counted by order of frequency.
• names.txt: 21,986 names
  This database contains the most common names used in the United
  States and Great Britain. Spelling checkers may want to supplement
  their basic word list with this one.
• names-f.txt: 4,946 female names
  frequent given names of females in English speaking countries
• names-m.txt: 3,897 male names
  frequent given names of males in English speaking countries
• oftenmis.txt: 366 often misspelled words
  many of the most commonly misspelled words in English speaking countries
• places.txt: 10,196 places
  a large selection of place names in the United States
• single.txt: 354,984 single words
  Over 354,000 single words, excluding proper names, acronyms, or
  compound words and phrases. This list does not exclude archaic words
  or significant variant spellings.
• usaconst.txt: USA Constitution
  The Constitution of the United States, including the Bill of Rights
  and all amendments current to 1993.

All the tests were run one time on my Broadwell i7-5950HQ CPU @ 2.90GHz, a quad-core hyperthreaded CPU supporting 8 threads.  This machine has 16GB of RAM.

I imported the results into an Excel spreadsheet, formatted it nicely, added some fields, and made some charts that I thought would reveal some trends.

All the source code, and the analysis Excel file, are available in my github repo.

Analysis & Discussion

Here’s the aggregations that I thought were interesting.  If you’d like to see more analysis, let me know specifics in the comments!  Or, just clone the github repo and start working with the data in the Excel file.

In the tables and charts below, I used “uos” to represent std::unordered_set, “set” to represent std::set, and trie to represent the custom trie.  This allows the tables and charts to be somewhat more concise.

Inserts

Data Structure	# insert wins	Min insert winning time	Max insert winning time	Min insert time difference	Average insert time difference	Max insert time difference	Average insert % improvement
set	162	142	117630	1	24322	134577	34
uos	94	111	2156	5	261	1406	33

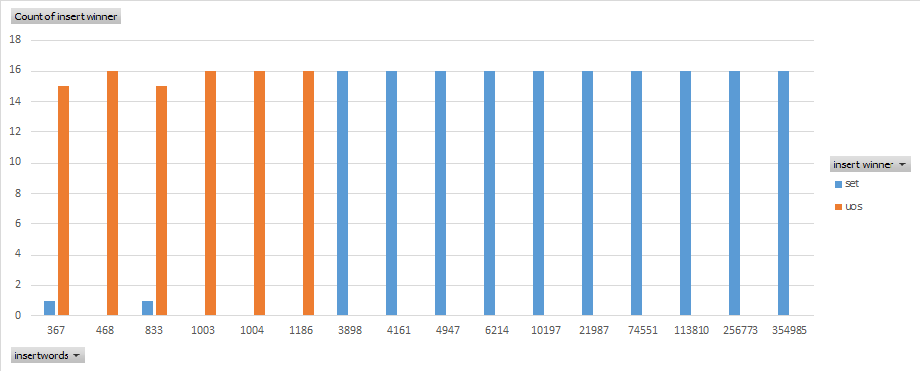
There is no typo or missing data here – the trie did not win a single test of insertion performance with this input data.  Std::set won about 63% of the tests while std::unordered_set won the other 37%.  We can see by the average percent improvement that when either data structure won, it outperformed the next best performer by an average of ~33%.  However, the min winning time, max winning time, average time difference, and max time difference seem to point to a conclusion that the std::set is faster at storing larger sets of strings, while maybe the std::unordered_set is faster at storing smaller sets of strings.

This chart, with number of strings stored in the set on the x-axis and number of wins on the y-axis, shows the trend precisely.  Std::unordered_set wins almost every test of small set size, while std::set wins every test of larger set size.

Deeper investigation shows that std::unordered_set wins in the files fiction.txt, freq.txt, freq-int.txt, kjvfreq.txt, oftenmis.txt, and usaconst.txt.  These files typically contain strings where each line contains a phrase of 1 – 3 words (1 – 20 chars), though usaconst.txt contains lines with long strings containing up to 60 or more characters.

Set wins in the files acronyms.txt, common.txt, compound.txt, crosswd.txt, crswd-d.txt, names.txt, names-f.txt, names-m.txt, places.txt, and single.txt.  These files contain short strings of 1 – 3 words, up to ~20 characters.

Since std::set is typically implemented using some kind of binary search tree, and std::unordered_set is typically implemented with an open hash (array of buckets, with each bucket containing a list) it appears that in these implementations there is lower initial overhead with a std::unordered_set, but worse asymptotic performance; there is higher initial overhead with std::set, but better asymptotic performance.  Perhaps the initial rebalances in the binary tree, especially when created using sorted data, are more expensive than filling the buckets in the open hash with very few items.  However, when the buckets start to accumulate multiple items per bucket and need to be searched linearly, the binary tree can be faster.

Finally, a trie appears to have both higher initial overhead than both std containers, and worse asymptotic insertion performance; this is probably because it potentially creates multiple new nodes for each inserted string, while the std containers probably create one new node per inserted string.

Search

Data structure	# search wins	Min search winning time	Max search winning time	Min search time difference	Average search time difference	Max search time difference	Average search % improvement
trie	200	2	49153	5	4066	31051	78
uos	56	28	80969	10	4481	101197	42

Again, no missing data in this table – std::set did not win a single search performance test.  In this data set, the trie wins approximately 78% of the tests while std::unordered_set wins the other approximately 22%.

The trends in this data are far less clear, so let’s take a closer look at some interesting charts.

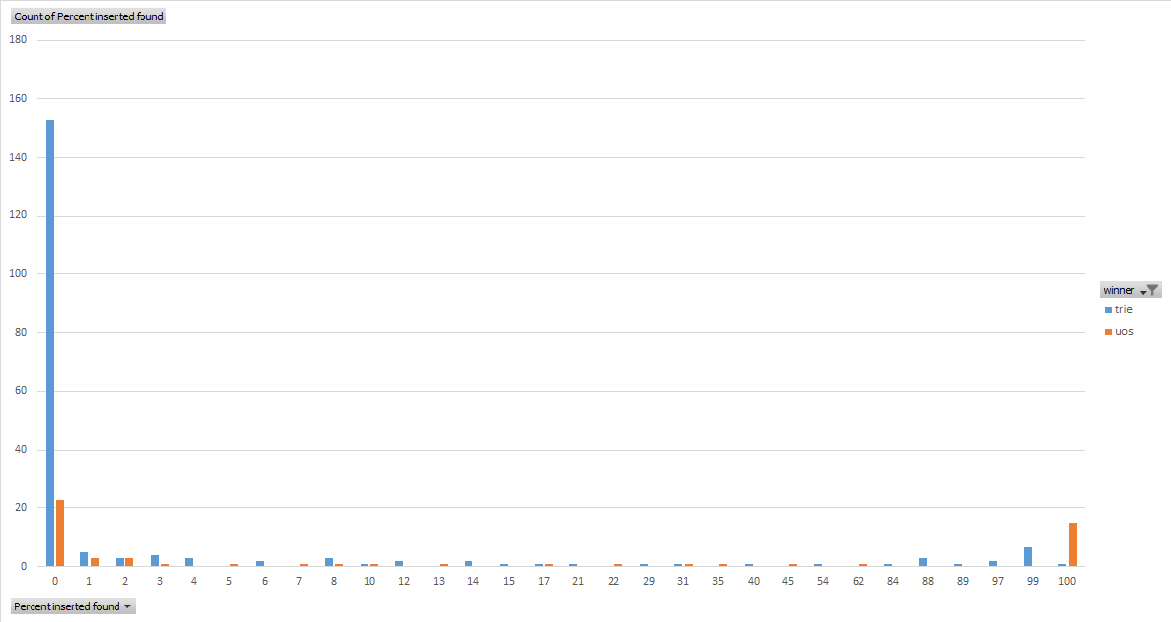
This one is a little hard to read but it’s got “percent of inserted strings found” on the x-axis and number of wins on the y-axis.

What this unsurprisingly shows is that when there’s very small intersection between the strings that were inserted and the strings that were searched for, the trie wins.  This could be because a trie can theoretically determine mismatch between a string and the dictionary with a single array element read.  For example, when comparing names.txt, which contains strings all starting with a capital letter, with freq-int.txt, which effectively contains strings starting with a number, the trie always finds that the first character of the search string has no branch in the trie’s root node, so it returns false very quickly.  On the other hand, when searching a binary tree, the search takes approximately log N time to reach a leaf and determine there’s no match.

On the other hand, when there’s a very large/complete intersection between the inserted strings and the search strings, the std::unordered_set wins.  This is again not too surprising, because the trie performs length(searchstring) array element reads which cannot be vectorized.  The binary tree must perform more than length(searchstring) character comparisons, but they can be vectorized.

So the vast majority of the trie’s search wins occur when there is very small intersection between the inserted strings and the search strings, for the obvious reason that it is very fast at determining that a search string starts with a letter that none of the inserted strings start with.  Here’s the data with those points removed, to get a better sense of general-purpose search performance:

Data structure	# search wins	Min search winning time	Max search winning time	Min search time difference	Average search time difference	Max search time difference	Average search % improvement
trie	47	11	49153	5	6223	27741	60
uos	33	51	80969	15	7361	101197	38

The trie still wins more tests than the std::unordered_set.  Also, in the search tests where it wins, it outperforms the next best performer by an average of 60%.  On the other hand, when std::unordered_set wins, it beats the next best performer by an average of 38%.

There’s a similar trend for “percent of searched strings found” and “winning search time” with possibly a slightly more visible trend of the trie performing better with small intersection of inserted & search sets, and std::unordered_set performing better with large/complete intersection.  Those charts are in the “search wins vs % searched found” and “search wins vs winning time” tabs of the Excel spreadsheet.

Conclusion

With many use cases, reads/searches are performed far more often than writes/inserts – think of financial transactions, event signups, online store orders, and more.  For this reason, it’s often preferable to optimize for read/search performance rather than write performance.

When performing search operations on a string set, it seems clear that the fastest data structures are either a custom trie or a std::unordered_set.  When the search data is expected to have a small intersection with the inserted data, such as looking for strings indicating malware in the output of the unix “strings” command, a trie is likely to be the fastest data structure.  When the search data is expected to have a large/complete intersection with the inserted data, such as the grader of a spelling test, a std::unordered_set is likely to be the fastest data structure.

However, there are use cases where write/insert performance is more important than read/search performance.  For example, an algorithm that finds unique strings in a data set by inserting them into a set ought to consider using std::set for this purpose.

A final note about these performance tests: it’s likely the std::set and std::unordered_set implementations are highly optimized, and may even have specialized template implementations for std::string.  The custom trie was written by a single developer in a couple of hours.  There could be a lot of room in the trie implementation for improvement.

Finally, there was no attempt during these experiments to measure the memory usage of the various data structures.  It’s very likely that the trie uses significantly more memory than either of the std containers, since each node uses an array of almost 100 ints, where 0 or more are used.  It’s a very sparse data structure.

So that’s it!  If you’re interested in this, please take a look at the github repo that contains all the source, and the Excel sheet  that contains the analysis.  Also, I’m always interested in discussions spurred on by my posts, and learning what I’ve done wrong or suboptimally.  So if you’d like to discuss or correct anything, please let me know by leaving a comment below!
.