Many problems in real life can be represented as optimization problems that are subject to various constraints. How far can I go without stopping at the gas station if I expect to drive 60% on the highway and 40% in the city? What’s the most enjoyment I can get with $10 of chocolate bars, given that I want at least one Butterfinger bar but like Snickers twice as much? How can I achieve the best GPA given my current grades in the classes, each class’s grading system, and that I only have 2 more days to study for finals?
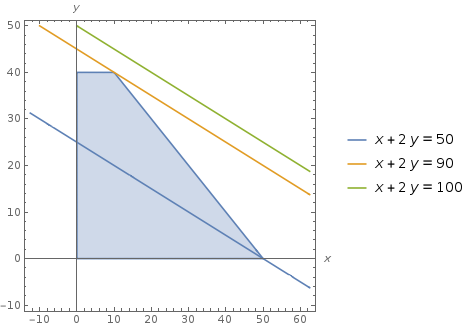
The simplex method is an algorithm for finding a maximal function value given a set of constraints. We’ll start with a non-trivial example that shows why we need a rigorous method to solve this problem, then move on to a simple example that illustrates most of the main parts of the simplex method. You’ll learn when to use it, you can check out my cheatsheet, and you can review my code on github!