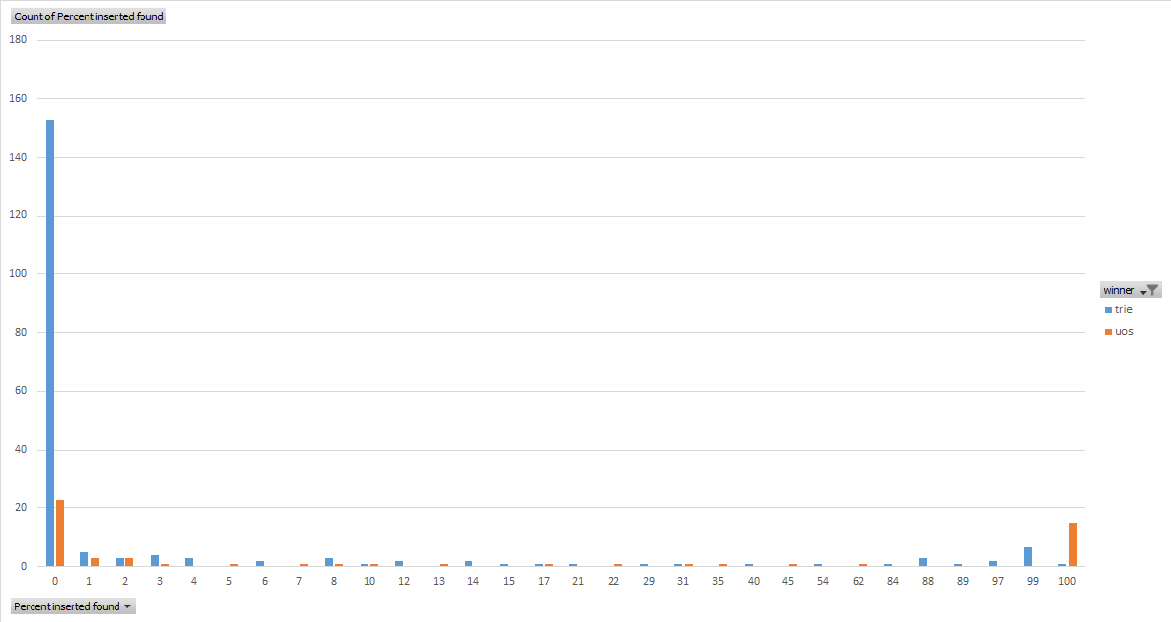
I recently interviewed with a large company where I was asked how I would check that a given word was a valid English word. Knowing that there were on the order of a few tens of thousands of stems, and that each stem may have many variations, I figured that there were maybe a few hundred thousand possible words in the English language. With each word having average length probably in the 7 range, there might be a million or so characters in this set. I concluded that the check could be performed by searching an in-memory dictionary, and proposed either a std::unordered_set, or a custom trie, with a performance test necessary to see which would be faster.
I decided to perform this test.